New solutions for capillary waves on fluid sheets

By M. G. BLYT H AND J.-M. VANDEN-BROECK
School of Mathematics, University of East Anglia, Norwich NR4 7TJ, UK

(Received 16 December 2003 and in revised form 11 March 2004)

The classical problem of nonlinear capillary waves on two-dimensional fluid sheets is reconsidered. The problem is formulated in terms of a complex potential, and solutions are sought using Fourier series expansions. A collocation technique combined with Newton's method is used to compute the Fourier coefficients numerically. Using this procedure, the exact solutions of Kinnersley (1976) are recomputed and various symmetric and antisymmetric wave profiles are presented, including the limiting configurations which exhibit trapped bubbles of air. Most important, three new solution branches which bifurcate nonlinearly from the symmetric Kinnersley solution branch are identified. The wave profiles along these new branches do not possess the symmetry or antisymmetry of the Kinnersley solutions, although their limiting configurations also display trapped air bubbles. No bifurcations are found along the antisymmetric Kinnersley solution branch.

1. Introduction

Crapper (1957) obtained exact nonlinear solutions for capillary waves on fluid sheets of infinite depth in terms of elementary functions. His results demonstrated that sharp troughs develop as the wave amplitude is increased until, ultimately, a limiting profile is reached with a trapped air bubble appearing at the trough. Beyond this point, the solutions intersect themselves and must be discarded on physical grounds. Later, Vanden-Broeck & Keller (1980) showed how the solutions could be extended beyond this limiting configuration by allowing the pressure in the trapped bubble to differ from the ambient pressure above the fluid. With a view to modelling the effect of a surfactant on the capillary waves, Vanden-Broeck (1996) numerically computed new solutions for variable surface tension using a collocation technique.

Taylor (1959) showed that small-amplitude surface waves on thin fluid sheets can exist either in a symmetric configuration, in which a trough on one surface opposes a peak on the other surface, or in an antisymmetric configuration, where a peak faces a trough, and presented some experimental results. Kinnersley (1976) generalized Crapper's analysis to the case of fluid sheets of finite thickness and obtained exact nonlinear solutions, which are the large-amplitude analogues of Taylor's linear waves. Kinnersley derived a dispersion relation for the finite-amplitude waves in terms of elliptic functions and showed that it reduced to Crapper's result in the limit of infinite depth. For fluid sheets of finite thickness, he demonstrated that a maximum wave amplitude is attained. Beyond this, the solutions self-intersect and lose physical significance. Very few waves profiles are shown in Kinnersley's paper, although the appearance of trapped bubbles is noted in the limiting case of thin sheets. Kinnersley's results were rederived in a simpler form by Crowdy (1999), who reconsidered the problem using a new complex variable approach.

In this paper, we readdress the problem of capillary waves on fluid sheets of finite thickness. We recompute typical symmetric and antisymmetric wave profiles corresponding to the exact Kinnersley solutions, with a view to clearly demonstrating the shape of finite-amplitude wave profiles up to the trapped-bubble limit. We follow a numerical approach based on an iterative point collocation method, adapted from that used by Vanden-Broeck (1996). In particular, we investigate the possibility of solutions without the symmetry or antisymmetry of the Kinnersley waves. A linearized analysis along the lines of Taylor (1959) shows that, for small-amplitude waves, there cannot be an arbitrary phase shift between the upper and lower surfaces, and only the symmetric and antisymmetric solutions are possible in this limit. However, by numerically tracing the symmetric solution branch into the nonlinear regime, we identify three new solution branches which emerge as bifurcations at finite amplitude. Typical wave profiles along these new branches are presented, and it is shown that along each new branch a limiting configuration is reached which features trapped bubbles of air. No bifurcations are found along the antisymmetric solution branch. Our new solutions are reminiscent of those computed by Chen & Saffman (1980) for pure gravity waves.

2. Problem formulation

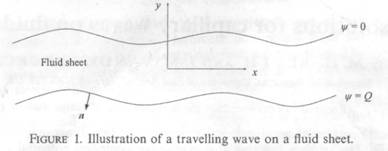
We reconsider the classical problem of a two-dimensional -sheet of fluid of finit thickness, surrounded by air, on which a train of periodic waves of wavelength A ar travelling at a constant speed, as shown in figure 1. We adopt a frame of reference ii which the fluid motion is steady. The fluid is assumed to be inviscid, incompressible and irrotational, so that the flow within the sheet is governed by Laplace's equation

We introduce a complex potential f = fi+ipsi, where fi(x, y) is the velocity potential and psi(x, y) is the stream function defined so that = 0 on the upper surface an( 1/r = Q, with Q < 0, on the lower surface. The wave speed c is defined by taking the average velocity u = grad fi over one period of a streamline, so that

where dx = (dx, dy). This implies that when x varies by an amount A over a wavelength, then _c varies by clamda. Since the flow is irrotational, c is the same for any choice of streamline. Choosing f to be analytic inside the fluid domain, it only remains to satisfy the normal stress balance at the upper and lower free surfaces. Thus, it is required that

where p is the fluid pressure, p_a is the atmospheric pressure, y is the surface tension, and K = div n is the surface curvature, with n the unit surface normal pointing downwards. Applying Bernoulli's equation at each surface, and using (2.2), (2.3), we have

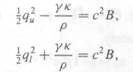
(2.4)

(2.5)

where q_t„ q_l are the fluid speeds on the upper and lower surfaces respectively, and p is the fluid density. The Bernoulli constant c^cB is to be determined. Exact solutions to this problem were given by Kinnersley (1976). These were later presented in a simplified form by Crowdy (1999). In the case of a semi-infinite fluid sheet, exact solutions were obtained by Crapper (1957). We compute solutions numerically using the collocation method of Vanden-Broeck (1996).

We work in the hodograp coordinates (fi,psi ). Defining the velocity components u = fi,x v = fi,y our goal is to compute u — iv as an analytic function of f . All computed waves are symmetric about 0 = 0. Introducing tau(fi,psi) — itheta(fi, psi), defined so that

(2.6)

we may express the surface curvature K as

(2.7)

Referring velocities to the wave speed c and lengths to the wavelength A, we now write variables as dimensionless quantities and seek solutions which are periodic in 0 with a unit period. According to the preceding definitions, (2.4) and (2.5) become

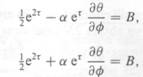
where the dimensionless parameter

is defined by

(2.8)

(2.9)

(2.10)

Following Vanden-Broeck & Miloh (1995), we express the solution in the form of an infinite series,

(2.11)

where a₀ and the coefficients a_n, bn are to be found. Note that all of these coefficients are real. This follows from the assumed symmetry about 0 = 0. Previous workers (Taylor 1959; Kinnersley 1976; Crowdy 1999) have computed both symmetric waves, where a trough on the upper wave opposes a peak on the lower wave, and antisymmetric waves, where a trough faces a trough. For the symmetric waves, by noting that

(2.12)

we see that the following relationship holds between the series coefficients:

Similarly, for the antisymmetric waves, by noting that

a similar relationship holds, namely,

(2.13) (2.14) (2.15)

Two distinct approaches to calculating the waves present themselves. First, we can adopt either of the formulae (2.13) or (2.15) and compute symmetric or antisymmetric waves. Second, we can make no prior assumptions about the coefficients and confirm the relationships (2.13) and (2.15) a posteriori. The latter approach leaves open the possibility of computing new solutions without any assumed symmetries.

2.1. Numerical method

In practice we must terminate the two series in (2.11) at a finite level. Fixing the surface tension parameter a, and truncating each series after N — 1 terms, we determine the 2N unknowns B, a₀ and an, bn, n = 1, ... , N — 1, by introducing N collocation points 0; along the upper wave, and N — 1 points 0; along the lower wave, with

(2.16)

Consistent with the non-dimensionalization introduced above, the final condition comes from demanding that x change by a unit amount over one period in 0. Thus, we demand that

(2.17)

Substituting (2.11) into the Bernoulli conditions (2.8) and (2.9) and condition (2.17) at each of the collocation points, we obtain 2N nonlinear algebraic equations

for the 2N unknowns

iteratively using Newton's method.

To fully characterizethe solutions, we denote non-dimensional arclength along the wave by s and introduce the new dimensionless parameter T, defined on the upper surface ip = 0 so that

The solution is obtained

(2.18)

which expresses the potential energy due to surface tension contained in the distorted surface (Schwartz & Vanden-Broeck 1979). In the case of a flat surface, T = O. With this definition, the dynamics is described by the two free parameters a and T. Once a solution has been computed, x and y are obtained by integrating the identity

3. Results

A first check on the numerical method is provided by recomputing the exact solutions of Crapper (1957) for waves on a fluid sheet of infinite depth. We obtained

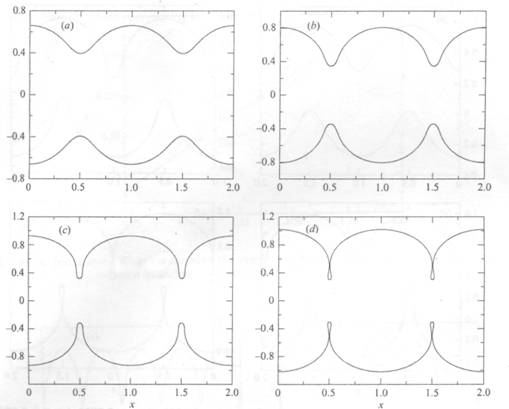
FIGURE 2. Q = —0.5. Symmetric waves for (a) a = 0.1013, (b) a = 0.1154, (c) a = 0.12949,
and (d) a = 0.14103, the limiting configuration with trapped bubbles.

excellent agreement with Crapper's dispersion relation between the wave speed and the wave steepness, that is the difference in height between a trough and a crest. To check the scheme for finite fluid sheets, the exact solutions of Kinnersley (1976) were recomputed. In figure 2 we display some of the possible waves in the symmetric configuration when Q = —0.5 for increasing values of the surface tension parameter a. In figure 3, some antisymmetric waves are shown for Q = —0.5 and various values of a. The numerical scheme was implemented first adopting the relationships (2.13) and (2.15), and then under general conditions. In the latter case, the relationships were confirmed numerically after convergence. For both the symmetric and antisymmetric waves, the computations are continued up to the limiting configuration with a small trapped air bubble. Continuing beyond this point, we obtain self-intersecting waves, which are of no physical relevance. To demonstrate convergence of the numerics.

decay rapidly with n.

A linearized analysis along the lines of Taylor (1959) reveals that, in the limit of small-amplitude periodic perturbations, only symmetric or antisymmetric disturbances are permitted. Therefore there cannot be an arbitrary phase shift between the upper and lower surface waves. However, this does not prevent other types of wave profile from appearing as nonlinear bifurcations from the symmetric or antisymmetric

we note that, for figure 3(a) where

with

we have

and so the coefficients a„, b„

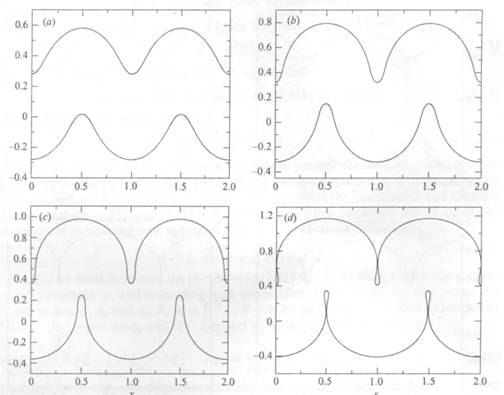
FIGURE 3. Q = —0.5. Antisymmetric waves for (a) a = 0.1853, (b) a = 0.2038, (c) a = 0.2223,
and (d) a = 0.2426, the limiting configuration with trapped bubbles.

solution branches. To investigate these, we follow the symmetric and antisymmetric solution branches and look for bifurcations at finite amplitude. Following the symmetric branch, we monitor the sign of the determinant of the Jacobian matrix, 1 V II, where the gradient is taken with respect to the unknowns fl. For illustrative purposes, we consider the case Q = —0.1. As the surface tension parameter a is varied, the determinant changes sign three times along the branch. This suggests the existence of bifurcation branches (e.g. Keller 1977). By computing the eigenvector corresponding to the numerically smallest eigenvalue of the Jacobian matrix at the point where the determinant changes sign, and aligning our initial guess for Newton's method with this eigenvector, we are able to step off the symmetric branch onto the new solution branch. This procedure was repeated at the other two bifurcation points. The resulting bifurcation diagram is displayed in figure 4. The new solution branches, which are shown as broken lines, are continued up to the point where the corresponding wave profiles exhibit a trapped bubble and thereafter self-intersect. We took N = 65 to accurately resolve the more intricate wave profiles. For example, on branch 1 in figure 4, when a = 0.2870 we compute T = 0.8250 with N = 15, T = 0.9230 with N = 35, T = 0.9238 with N = 55, and T = 0.9238 with N = 65. For the simpler profiles, far fewer modes are required. The wave profiles on branches 1, 2 and 3 can be seen in figures 5, 6 and 7 respectively. Concerning secondary bifurcations from these new solution branches, we note that the determinant of the Jacobian matrix remains single-signed along each of these branches up to the point of self-intersecting profiles.

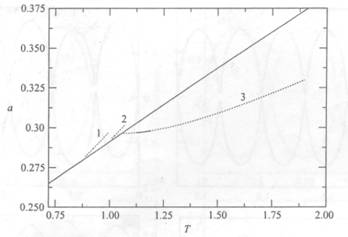
FIGURE 4. Bifurcation diagram showing the symmetric branch (solid line) and the three new
solution branches (broken lines) for the case Q = —0.1.

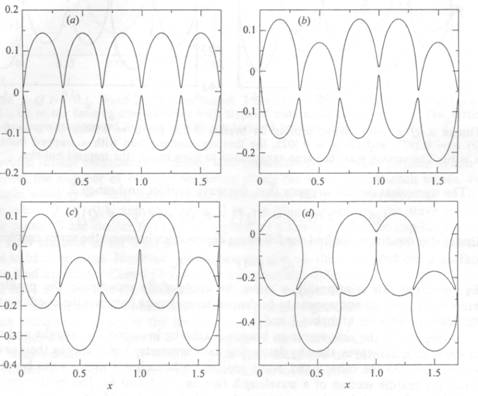
FIGURE 5. Q = —0.1. Wave profiles on branch 1 for (a) a = 0.2783, (h) a = 0.2794, (c) a = 0.2840, and (d) a = 0.2943, the limiting configuration with a trapped bubble at x = 1.0. The vertical scale has been exaggerated to show clearly the trapped bubbles.

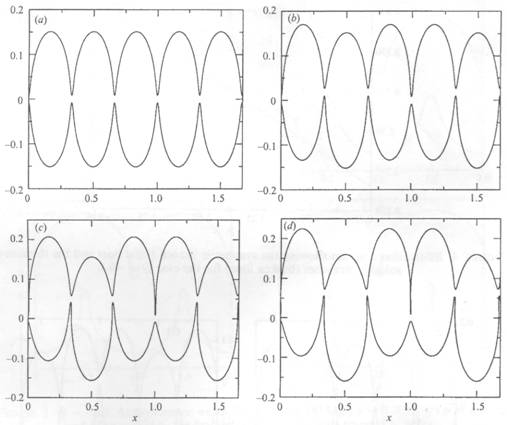
FIGURE 6. Q = —0.1. Wave profiles on branch 2 for (a) a = 0.2900, (b) a = 0.2913, (c) a = 0.2977, and (d) a = 0.3025, the limiting configuration with a trapped bubble at x = 1.0. The vertical scale has been exaggerated to show clearly the trapped bubbles.

The numerical output suggests that, for wave profiles on branch 2,

(3.1)

Under this condition, we find the following dependence between the series coefficients:

(3.2)

By assuming this relationship a priori, we successfully recompute the profiles on branch 2. There do not appear to be simple dependences between the coefficients for the wave profiles on branches 1 and 3.

Topologically, the new waves on branch 3 arise by lowering the troughs and crests of the symmetric waves, thereby destroying their symmetry but retaining their original wavelength. On the other hand, wave profiles on branches 1 and 2 arise by pulling down the middle section of a wavelength (see figures 5 and 6). The main symmetric branch in figure 4 has been computed so that one period in ₀ contains three wavelengths (see figure 5(a), for example). As a result, the only non-zero coefficients a_n, b„ occur if n = 0 (mod 3). Computationally, there is the possibility of obtaining new bifurcation branches with topologically different profiles when m wavelengths are included within one ₀ period along the main symmetric branch; in this case, the only non-zero coefficients occur if n = 0 (mod in). However, our investigations have not

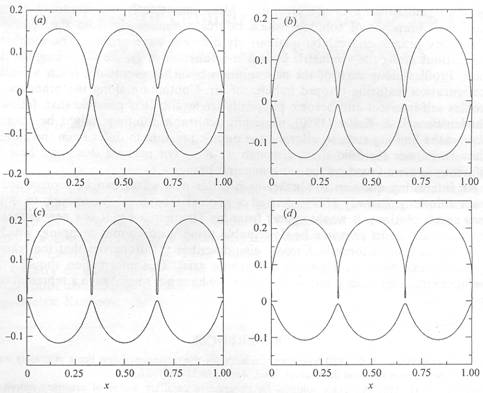
FIGURE 7. Q = —0.1. Wave profiles on branch 3 for (a) a = 0.2960, (6) a = 0.2990, (c) a = 0.3083, up to the limiting eonfiguration with trapped bubbles at (d) a = 0.3176. The vertical scale has been exaggerated to show clearly the trapped bubbles.

uncovered further bifurcation branches with qualitatively new wave profiles. When Q is varied, the number of bifurcation points along the symmetric branch varies. For example, when Q = —0.4, there are no bifurcations; there are two when Q = —0.2, three when Q = —0.1, and one when Q = —0.05. Interestingly, the wave profiles along branch 3 are similar to those computed by Crowdy (2001) for capillary waves on a fluid annulus in the limit as the number of waves packed around the annulus tends to become large. However, the surface tension on the inner and outer surfaces of the fluid annuli for Crowdy's solutions are generally different.

We have also looked for bifurcations from the antisymmetric Kinnserley branch. The determinant of the Jacobian matrix remains single-signed along the antisymmetric branch when m = 3, up to the limiting configuration with a trapped bubble. The same is true when in = 4 and m = 5. We repeated these calculations for several values of Q with similar results. It would appear that there are no bifurcations from the antisymmetric branch, and hence no additional new solutions.

4. Summary

We have adapted the Fourier-series-based numerical method of Vanden-Broeck & Miloh (1995) to computing nonlinear capillary waves on fluid sheets of finite thickness. The numerical code was tested by recomputing the exact solutions of Crapper (1957) and Kinnersley (1976). An assortment of profiles for both symmetric

264 M. G. Blyth and J.-M. Vanden-Broeck

and antisymmetric waves are presented. More importantly, we identified at most three new branches of solution, which bifurcate nonlinearly from the symmetric Kinnersley branch and exhibit qualitatively different wave profiles. The number of bifurcations along the symmetric branch is a function of Q, the flux along the fluid sheet. Profiles along each of the new solution branches eventually reach a limiting configuration featuring trapped bubbles of air. Continuing along the branches, the profiles self-intersect and become physically irrelevant. It is possible that, following Vanden-Broeck & Keller (1980), physically realizable solutions might be obtained beyond the limiting state by allowing the bubble pressure to differ from the ambient pressure outside the fluid sheet, although we have not pursued this point here. No bifurcations were found on the antisymmetric branch.

An interesting question is whether or not our new waves can be represented by exact solutions. Crowdy (1999) derived a general theoretical framework to obtain such exact solutions. It would appear from his Theorem 2.4 that our new numerical solutions should in principle be describable using a conformal mapping, which is given by an explicit formula. Crowdy also describes the properties that the relevant conformal mappings must possess if solutions exist. This information should prove useful in obtaining exact solutions. However, we have not sought such a representation here.

REFERENCES

CHEN, B. & SAFFMAN, P. G. 1980 Numerical evidence for the existence of new types of gravity waves of permanent form on deep water. Stud. Appl. Maths 62, 1-21.

CRAPPER, G. D. 1957 An exaet solution for progressive capillary waves of arbitrary amplitude. J. Fluid Mech. 2, 532-540.

CROWDY, D. G. 1999 Exact solutions for steady capillary waves on a fluid annulus. J. Nonlinear Sci. 9, 615-640.

CROWDY, D. G. 2001 Steady nonlinear capillary waves on curved sheets. Eur. J. Appl. Maths 12, 689-708.

KELLER, H. B. 1977 Applications of Bifurcation Theory. Academic.

KINNERSLEY, W. 1976 Exact large amplitude waves on sheets of fluid. J. Fluid Mech. 77, 229-241. SCHWARTZ, L. W. & VANDEN-BROECK, J.-M. 1979 Numerieal solution of the exact equations for capillary-gravity waves. J. Fluid Mech. 95, 119-139.

TAYLOR, G. I. 1959 The dynamics of thin sheets of fluid. II. Waves on fluid sheets. Proc. R. Soc. Lond. A 253, 296-312.

VANDEN-BROECK, J.-M. 1996 Capillary waves with variable surface tension. Z. Angew Math. Phys. 47, 799-808.

VANDEN-BROECK, J.-M. & KELLER, J. B. 1980 A new family of eapillary waves. J. Fluid Mech. 98, 161-169.

VANDEN-BROECK, J.-M. & MILOH, T. 1995 Computations of steep gravity waves by a refinement of Davies-Tulin's approximation SIAM J. Appl. Maths 55, 892--903.